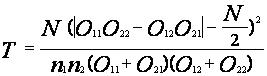Содержание

2.5.3. Обучающий этап эксперимента

Обучающий этап эксперимента был проведен в 2001-2002 учебном году на механико-технологическом факультете Новосибирского государственного технического университета. Экспериментальное обучение проводилось в группах: МХ-11, МХ-12, ММ-11, МЭ-11 (63 студента).  В качестве контрольных групп были выбраны группы: КМ-11, КП-11, ТМ-12, МП-11 (68 студентов).

Цель этого этапа эксперимента состояла в определении эффективности обучения начертательной геометрии студентов технического вуза по разработанной автором технологии. Основным критерием эффективности было принято качество знаний и умений студентов по начертательной геометрии. Гипотезой эксперимента было следующее предположение: применение разработанной технологии при обучении начертательной геометрии повышает качество предметной подготовки студентов технического вуза. Критерием качества  мы считали уровень овладения программным учебным материалом. В качестве показателей были взяты школьные итоговые отметки по геометрии и экзаменационные отметки по НГ.

Для сравнения качества предметной подготовки оценивалась доля Р студентов, сдавших экзамен по НГ на «хорошо» и «отлично».  Перед началом эксперимента в контрольных  и экспериментальных группах доли «хорошистов» были равны (0,94), судя по школьным итоговым отметкам по геометрии. После экспериментального обучения количество студентов, сдавших экзамен на «отлично» или «хорошо» составило 48 человек (из 63), т.е. Р_э=f_э/n_э = 0,76, где f_э – число студентов экспериментальных групп, сдавших экзамен на «отлично» и «хорошо», а  n_э – общее число студентов экспериментальных групп. Соответственно в контрольных группах отметку «отлично» или «хорошо» получили 35 студентов (f_к) из 68 (n_к), т.е. Р_к = 0,51.  Данные рассчитаны на основе таблиц 1 и 2 (см. приложение 10).

По этим данным проверим гипотезу Н₀: Р_э = Р_к, при альтернативной гипотезе Н₁: Р_э ≠ Р_к. Вычислим статистику z по формуле [21, с. 295]:

Для экспериментальных данных z = 2,89. Это значение превышает критическое значение _0,975 z = 1,96 для a = 0,05. Такой результат дает основание отклонить нулевую гипотезу Н₀: Р_э = Р_к и принять альтернативную гипотезу Н₁: Р_э ¹ Р_к. Так как Р_э > Р_к, то можно сделать вывод, что применение экспериментальной технологии индивидуализации обучения НГ с элементами дистантной системы образования повышает качество предметной подготовки студентов технического вуза.

Сопоставление экзаменационных оценок по начертательной геометрии и линейной алгебре показало, что в экспериментальной группе доли «хорошистов» и «отличников» по этим предметам существенно отличаются (0,71 и 0,48 соответственно), а в контрольной группе качественные показатели отличаются незначительно (0,51 и 0,54). Это дополнительно указывает на эффективность разработанной технологии.

Для проверки прочности знаний в сентябре 2002 года была проведена отсроченная контрольная работа (образец варианта приведен в приложении 11). При решении предложенных задач, студенты должны были продемонстрировать знания, умения и навыки, необходимые для решения позиционных и метрических задач. Максимальное число баллов, которое можно было получить за правильное решение задачи 1, равно 7 баллам, задачи 2 – 10 баллам, задачи 3 – 24 баллам.

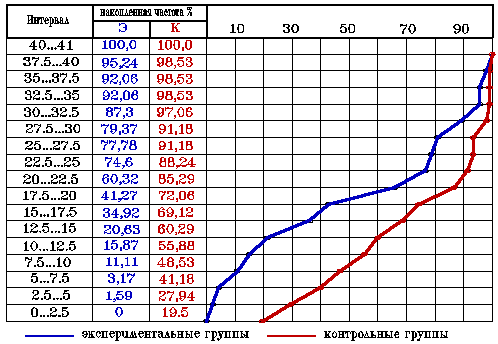
а)  Гистограмма результатов отсроченной контрольной работы б) Кривая процентилей (огива) итогов отсроченной контрольной работы Рисунок16. Итоги отсроченной контрольной работы

Максимальное количество баллов за всю работу – 41, при переводе в четырехбалльную систему использовалось следующее соотношение:

1) «неудовлетворительно» – менее 11 баллов;

2) «удовлетворительно» – от 11 до 20 баллов;

3) «хорошо» – от 21 до  30;

4) «отлично» ­– свыше 30 баллов.

На выполнение работы отводилось 90 мин.

Обработка результатов выполнения отсроченной контрольной работы (КР) по экспериментальным и контрольным группам приведена в приложении 12.

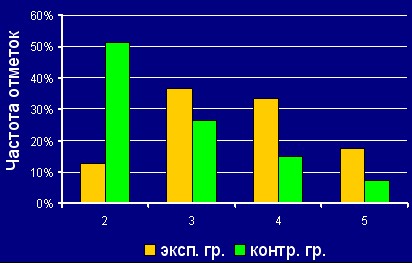
Результаты выполнения отсроченной КР по экспериментальным и контрольным группам приведены  в таблице 1 и на рис.16.

Таблица 1

Приведенные данные свидетельствуют о более прочном усвоении знаний в экспериментальных группах по сравнению с контрольными.

Чтобы сопоставить уровень остаточных знаний с успешностью работы в семестре, были отобраны отметки за контрольные и графические  задания по темам, знания которых необходимы для решения отсроченной контрольной работы.

К ним относятся:

1)            тест-контроль по теме «Точка»;

2)            тест-контроль по теме «Прямая»;

3)            тест-контроль по теме «Плоскость»;

4)            тест-контроль по теме «Поверхность»;

5)            контрольная работа по теме «Точка, прямая, плоскость»;

6)            графическое задание по теме «Точка, прямая, плоскость»;

7)            две задачи на взаимное пересечение поверхностей.

Таким образом, максимальная сумма отметок составила 40 баллов, для оценки семестровой работы использовались такие же соотношения как и для отсроченной КР. Результаты представлены в Приложении 13.

Анализ результатов показал, что отметка за отсроченную КР не стала ниже семестровой в экспериментальных группах у 22 студентов, а в контрольных – у 10 человек.

Используем критерий χ² (хи-квадрат) для сравнения распределения объектов двух совокупностей по состоянию этого свойства (успеваемость). Имеются две совокупности объемом n₁= 63 и n₂ = 68, где n₁ и n₂ – число студентов в экспериментальных и контрольных группах соответственно. Шкала наименований изучаемого свойства имеет только две взаимоисключающие категории. По результатам измерений состояния изучаемого свойства у объектов двух выборок составлена таблица 2. В этой таблице  О₁₁ – число студентов экспериментальной группы, у которых отметка за отсроченную КР не стала ниже семестровой, О₁₂ – у которых она стала ниже; О₂₁ – число студентов контрольной группы, у которых отметка не снизилась, О₂₂ – у которых она стала ниже; N –общее количество студентов участвующих в эксперименте.

Для применения критерия выполнены все необходимые требования:

1)      обе выборки случайные;

2)      выборки независимы, и члены каждой выборки также независимы между собой;

3)      шкала измерений является простой шкалой наименований с двумя категориями.

Вероятность того, что случайно выбранный из экспериментальной группы студент будет принадлежать первой категории шкалы измерения проверяемого свойства, обозначим Р_Э. Вероятность того же события для контрольной группы обозначим Р_К. Тогда на основе данных таблицы 2 проверим для одностороннего критерия нулевую гипотезу Н_о: Р_Э≤Р_К при альтернативной гипотезе Н₁: Р_Э >Р_К.

 Таблица 2

Если хотя бы одна из абсолютных частот имеет значение, заключенное в пределах от 5 до 10, то применение критерия возможно при использовании для подсчета значения статистики формулу [23, С. 99]:

Таким образом, статистика, полученная на основании экспериментальных данных Т= 6,185.  Для α = 0,05 при числе степеней свободы υ=1 критическое значение статистик χ_1-2α, имеющих распределение χ², равно 3,841. Т.е.  Т > χ_1-2α, следовательно, нулевая гипотеза Р_Э≤Р_К отклоняется и принимается альтернативная Р_Э>Р_К. Вероятность того, что случайно выбранный студент экспериментальной группы будет принадлежать первой категории шкалы измерения проверяемого свойства, выше, чем вероятность того же события для контрольной группы

Таким образом, гипотеза исследования подтверждается результатами эксперимента.

Выводы по второй главе:

1. В основе разработанной автором технологии обучения начертательной геометрии студентов технических вузов лежит идея индивидуализации целей обучения, содержания учебного материала и введения элементов дистантной системы образования в процессуальную часть технологии.

2. Эффективность использования разработанной системы индивидуализированных задач по начертательной геометрии достигается необходимым соблюдением двух групп требований к этой системе: первая – обеспечивает систематизацию задач, а вторая – их индивидуализацию.

3. Особенностями структуры электронного учебного пособия, позволяющими использовать его в технологии индивидуализированного обучения с элементами ДСО студентов, являются представление учебной информации в мультимедийных лекциях с различной степенью подробности и наглядности; сопровождение практикума по решению типовых задач образцами их пошагового решения; введение критериев рейтинговой оценки, индивидуализация графических задач, наличие прикладной графической программы для просмотра моделей рисунков.

4. Результаты педагогического эксперимента подтвердили гипотезу исследования о том, что использование технологии индивидуализированного обучения с элементами дистантной системы образования способствует повышению качества обучения начертательной геометрии студентов технических вузов.

Начало

Далее