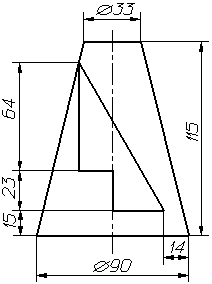
а)
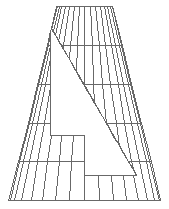
б)

в)
Рисунок 2. Условие задачи «Конус с призматическим отверстием»
а) двумерное изображение; б) каркасная модель; в) тонированная модель
В начертательной геометрии рассматривается два типа отношений между геометрическими фигурами: позиционные и метрические. Изучение теории и алгоритмов решения позиционных и метрических задач в трехмерном расширенном евклидовом пространстве направлено на развитие «пространственного мышления» студентов для дальнейшего чтения и сопоставления чертежей трехмерных объектов как на бумаге, так и на экране монитора. Следует заметить, что любая форма детали машины или механизма состоит из дуг и отсеков абстрактных геометрических фигур (прямых и кривых линий, плоскостей, сфер, цилиндров, конусов и т.д.). Поэтому для их конструирования, изображения, варьирования формой и размерами необходимо уметь синтезировать их из абстрактных геометрических тел, строить линии пересечения ограничивающих деталь поверхностей, определять принадлежность тех или иных точек и линий граням и поверхностям детали.
В НГ позиционными задачами принято называть такие, в которых требуется определить положение фигуры относительно плоскостей проекций и взаимное положение (принадлежность, параллельность, пересечение) двух и более фигур.
Положение фигуры по отношению к плоскостям проекций и изменение его для решения метрических задач рассматривается в теме «Точка, прямая, плоскость и поверхность».
Навыки определения взаимного положения простейших геометрических фигур: точки и прямой, двух прямых, точки и плоскости, прямой и плоскости, двух плоскостей формируются при решении типовых задач на практических занятиях. Рассмотрение позиционных задач с более сложными геометрическими фигурами включено в индивидуальные графические задания.
Построение линии пересечения поверхностей является наиболее интересной и часто встречающейся в инженерной практике позиционной задачей. Она решается с использованием метода вспомогательных секущих поверхностей – посредников, правильный выбор которых определяет рациональность последующих геометрических построений. В качестве поверхностей-посредников обычно используют плоскости и сферы. При выборе посредников исходят из того, чтобы они пересекали изучаемые поверхности по графически простым линиям – прямым и окружностям.
При решении подобных задач студент осваивает следующие обязательные умения: выбора опорных точек, поверхности-посредника, нахождения проекций точек линии пресечения и определения ее видимости. К умениям повышенного уровня можно отнести переход от плоского к наглядному изображению, построение наложенных сечений проецирующей плоскостью, плоскостью общего положения, определение их натуральной величины.
Система задач индивидуального графического задания по теме «Пересечение поверхностей» представляют собой единое целое, элементы которого объединены отношением принадлежности к теме, и включает в себя 9 типов задач:
1) цилиндр с призматическим отверстием;
2) конус с призматическим отверстием;
3) шар с призматическим отверстием;
4) пересечение двух цилиндров;
5) пересечение цилиндра и конуса;
6) пересечение цилиндра и шара;
7) пересечение составной поверхности и цилиндра;
8) пересечение составной поверхности и конуса;
9) пересечение составной поверхности и шара.
В задачах 1, 2, 3 требуется графически определить проекции точек линии пересечения поверхностей второго порядка с призмой; в задачах 4, 5, 6 – линию пересечения двух поверхностей второго порядка; в задачах 7, 8, 9 –линию пересечения поверхности второго порядка с составной поверхностью, включающей отсек поверхности второго порядка и многогранник. Очевидно, что предложенная система удовлетворяет требованию предшествования менее сложных задач более сложным.
Все типы задач имеют три уровня сложности. Например, в базовом уровне задачи «Конус с призматическим отверстием» требуется на основании исходных данных построить три проекции конуса с призматическим отверстием и сечение в натуральную величину проецирующей плоскостью, заданной преподавателем. Повышенному уровню сложности соответствует добавление к базовому уровню построения развертки поверхности конуса, высокому – дополнение первых двух построений диметрическим изображением. По каждому уровню имеются образцы оформления решения (см. приложение 2).
Исходные данные всех задач темы представлены с учетом уровня развития ПМ. Они обязательно включают в себя двумерное изображение. Для того чтобы учесть различия в уровнях развития ПМ студентов каждое условие дополнено каркасной и тонированной моделями заданной фигуры с возможностью просмотра изображения в графическом редакторе bCAD (рис.2). Обращение к гиперссылке своего варианта позволяет студенту увидеть каркасную статическую модель фигуры с возможностью перехода в режим тонированного просмотра и изменения точки отсчета.
|
а) |
 б) |
 в) |
|
Рисунок 2. Условие задачи «Конус с призматическим отверстием» а) двумерное изображение; б) каркасная модель; в) тонированная модель |
||
Задачи 1 – 6 также дополняются словесным алгоритмом решения, представленным в лекциях, который по желанию студента может быть дополнен пошаговой демонстрацией решения на компьютере. В процессе просмотра решения студент имеет возможность управлять скоростью и направлением смены кадров. Это позволяет учесть индивидуальную скорость усвоения учебного материала студентом.
Например, решение базового уровня задачи «Пересечение двух цилиндров» заключается в графическом нахождении проекций точек линии пересечения поверхностей на трех проекциях по предложенным исходным данным: двумерному изображению и моделям (рис. 3). Повышенный уровень сложности предусматривает построение сечения проецирующей плоскостью в натуральную величину, а высокий – дополнительное выполнение наложенных сечений. Пример пошаговой демонстрации решения базового уровня задачи, и образцы оформления задачи в соответствии с уровнем приведен в приложении 3.
|
а) |
б)
в) |
|
Рисунок 3. Условие задачи №4 «Пересечение двух цилиндров» а) двумерное изображение; б) каркасная модель; в) тонированная модель |
|
Задачи 7 – 9 относятся к эвристическим, т.к. алгоритм решения их не известен студенту, а составляется им самостоятельно с помощью разбиения исходной задачи на подзадачи. Условия задач представлены аналогично предыдущим – двумерным изображением (рис.4 а) и моделями (рис.4 б, в).
При решении каждой задачи студенту предоставляется возможность выбрать инструмент выполнения решения: традиционные чертежные инструменты или графический редактор bCAD.
Использование графического редактора позволяет проверить правильность результата сравнением его с решением, выполненным автоматически соответствующими инструментами bCAD (см. приложение 4).
Индивидуализация задач по другим темам проведена аналогично.
|
а) |
б)
в) |
|
Рисунок 4. Условие задачи №7 «Пересечение составной поверхности и цилиндра» а)двумерное изображение; б) каркасная модель; в) тонированная модель |
|