построение касательной и нормали к плоской кривой
|
построение касательной и нормали к плоской кривой |
Касательной к кривой линии называется прямая, представляющая предельное положение секущей.
На рисунках 85 и 86 представлены алгоритмы построения касательной к плоской кривой линии соответственно параллельно направлению и из точки, не принадлежащей кривой.
|
|
 |
|
|
|
Рисунок 85. Касательная к кривой
|
Рисунок 86.
Касательная к кривой
|
||
|
Рисунок 87. Касательная в точке кривой |
|
Для построения касательной в точке плоской кривой как видно из рисунка 87 используется две секущие хорды. Рассмотрим построение касательной в точке А. Для этого проведем секущие хорды АЕ и АD. Если точку Е приближать к точке А, секущая АЕ поворачивается вокруг точки А. Когда точка Е совпадет с точкой А (А≡Е) секущая АЕ достигнет своего предельного положения t. В этом предельном положении секущая называется полукасательной к кривой а в точке А. Секущая АD в предельном положении А≡D также представлена полукасательной t.
Кривая линия в точке А имеет две полукасательные прямые, которые совпадают и определяют одну касательную к кривой линии в точке А – кривая в этой точке называется гладкой (плавной).
Кривая плавная во всех её точках называется гладкой (плавной) кривой линией.
На кривой линии могут быть точки, в которых разнонаправленные полукасательные не принадлежат одной прямой, а составляют между собой угол. Так на кривой а в точке В угол δ между полукасательными не равен 1800. Точка В в этом случае называется точкой излома или выходящей точкой.
Нормалью п в точке А кривой линии называется перпендикуляр к касательной (рис.87).
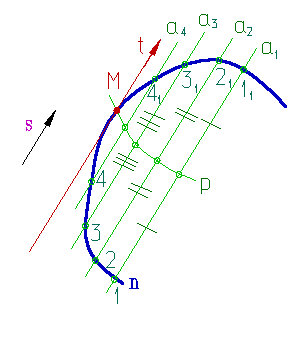
Построение нормали к кривой проходящей через точку А, не принадлежащую кривой m, можно выполнить следующим образом (рис.88):
|
Рисунок 88. Построение нормали к кривой |
|
1. Проведем окружности а1, а2, а3, а4, разных радиусов с центром в точке А;
2. Отметим точки пересечения окружностей с кривой -1, 11, 2, 21, 3, 31, 4, 41;
3. Из концов хорд восстановим перпендикуляры (при этом перпендикуляры, восстановленные из точек 1, 2, 3, 4, имеют противоположное направление перпендикулярам, восстановленным из точек 11, 21, 31, 41);
4. На полученных перпендикулярах отложим отрезки, равные длине соответствующих хорд;
5. Полученные точки соединим плавной кривой l;
6. Пересечение кривых m и l определит положение точки К, через которую пройдет искомая нормаль n.