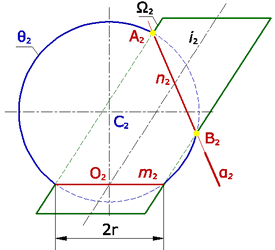
Рассмотрим пример пересечения поверхностей, для которого справедлива эта теорема.

Фронтальные проекции Q₂ сферы Q и W₂ эллиптического цилиндра W имеют общую окружность m(m₂) с центром О(О₂).

Плоскость σ, определяемая центром сферы С и осью i цилиндра, является плоскостью симметрии заданных поверхностей и параллельна фронтальной плоскости проекций.

Общая окружность радиуса r – это одна из плоских кривых 2-го порядка распавшейся линии пересечения. Остается построить вторую кривую, плоскость α которой должна быть в условиях данного примера перпендикулярна плоскости симметрии σ, а следовательно, и фронтальной плоскости проекций. Вторая линия пересечения (окружность) проецируется на фронтальную плоскость проекций в виде отрезка прямой n₂. Для ее построения следует воспользоваться точками А и В, принадлежащими очеркам заданных поверхностей.