|
|
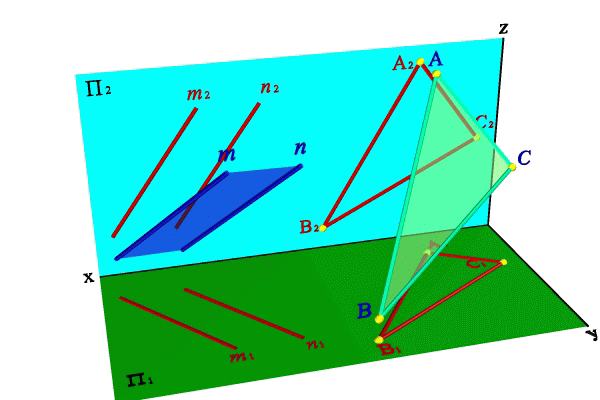
Задача. Дано: две плоскости общего положения a(m,n) и b (ABC). Требуется построить линию пересечения плоскостей a и b. Рассмотрим последовательность построения линии пересечения плоскостей a(m,n) и b(АВС). Проведем вспомогательные секущие плоскости g и d. Найдем линии пересечения этих плоскостей с заданными плоскостями. Плоскость g пересекает плоскость a по прямой (1, 2), а плоскость b – по прямой (3, 4). Точка пересечения этих прямых К одновременно принадлежит трем плоскостям a, b и g, т.е. искомой линии пересечения плоскостей a и b. Плоскость d пересекает плоскости a и b по прямым (5, 6) и (7, C), точка их пересечения М расположена одновременно в трех плоскостях a, b, d и принадлежит прямой линии пересечения плоскостей a и b. Таким образом, прямая (КМ) является линией пересечения плоскостей a и b. |