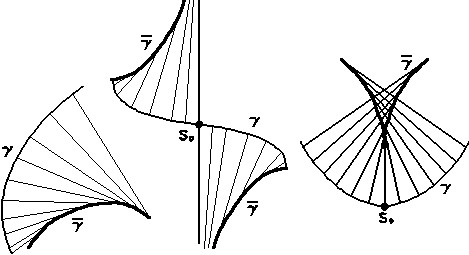
Эволюта* (от лат. evolutus - развернутый) - множество g¯ точек центров кривизны кривой g. Если r = r(s) (где s - натуральный параметр) - уравнение кривой g, то уравнение её эволюты имеет вид r¯= r + v/k, где k = k(s) - кривизна, v - нормаль кривой g. На рис. показано строение эволюты в трех характерных случаях:

а) вдоль всей кривой производная k`(s) знакоопределена, k(s) не обращается в нуль;

б) вдоль всей кривой производная k`(s) знакоопределена, k(s) обращается в нуль при s = s₀;

в) если s<s₀, то k`(s)>0, если s>s<sub>0</sub>, то k`(s)<0, k не обращается в нуль (точка эволюты соответствующая  s = s₀, является точкой возврата). Длина отрезка эволюты, соответствующего отрезку s₁≤ s ≤ s₂ кривой , равна  s¯(s₁s₂)=|1/k(s₁) - 1/k(s₂)|.

Эволюта является огибающей нормалей кривой g. Кривая g по отношению к своей эволюте называется эвольвентой.

Понятие эволюты и термин введены Х. Гюйгенсом (1673).

* Математический энциклопедический словарь./ Гл. ред. Ю.В. Прохоров; Ред. кол.: С.И. Адян, Н.С. Бахвалов, В.И. Битюцков, А.П. Ершов, Л.Д. Кудрявцев, А.Л. Онищик, А.П. Юшкевич.- М.: Сов. энциклопедия, 1988. - 847 с., ил