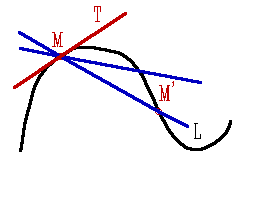
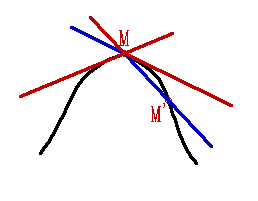
Касательная* к кривой линии - прямая, представляющая предельное положение секущей. Пусть М точка кривой L (рис. 1). На L выбирается вторая точка М' и проводится прямая ММ'. Точка М считается неподвижной, а точка М'  приближается к М по кривой L. Если при неограниченном приближении М'  к М прямая ММ'  стремиться к определенной прямой МТ, то МТ - называется касательной к кривой L в точке М. Но не у всякой непрерывной кривой имеются касательные, поскольку прямая ММ' может не стремиться к предельному положению или может стремиться к двум разным предельным положениям, когда М' стремиться к М с различных сторон от М (рис. 2). Встречающиеся в элементарной геометрии кривые имеют вполне определенную касательную во всех точках, кроме некоторого числа "особых" точек. Если кривая на плоскость в прямоугольных координатах определяется уравнением y=f(x) и f(x) дифференцируема в точке x₀, то угловой коэффициент касательной в точке М с абсциссой x₀ равен значению производной f '(x) в точке x₀; уравнение касательной в этой точке имеет вид: y-f(x₀)=f '(x₀)(x-x₀).

Касательной (прямой) к поверхности S в точке М называют любую прямую, проходящую через точку М и лежащую в касательной плоскости к S в точке М.

Рисунок 1.	Рисунок 2.

* Математический энциклопедический словарь./ Гл. ред. Ю.В. Прохоров; Ред. кол.: С.И. Адян, Н.С. Бахвалов, В.И. Битюцков, А.П. Ершов, Л.Д. Кудрявцев, А.Л. Онищик, А.П. Юшкевич.- М.: Сов. энциклопедия, 1988. - 847 с., ил