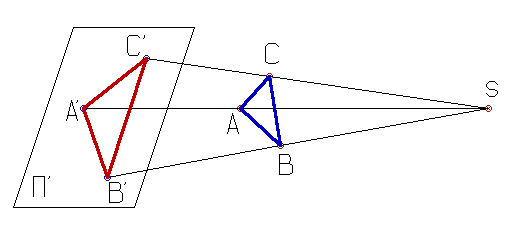
Проекция* (от лат. projectio — бросание вперёд, выбрасывание) — термин, связанный с операцией проектирования (проецирования), которую можно определить следующим образом (рис. 1): выбирают произвольную точку S пространства в качестве центра проектирования и плоскость П’, не проходящую через точку S в качестве плоскости проекций (картинной плоскости). Чтобы спроектировать точку А (прообраз) пространства на плоскость П’, через центр проекций S (глаз) проводят прямую SА до её пересечения в точке А’ с плоскостью П’. Точку А’ (образ) и называют проекцией точки А.

Проекцией фигуры F называется совокупность проекций всех её точек.

Прямая линия, не проходящая через центр проектирования, проектируется в виде прямой. Описанная проекция носит название центральной или конической. Она существенно зависит от  выбора центра проекций S. При проектировании точек данной плоскости П на плоскость П’ (рис. 2) встречаются следующие затруднения. На плоскости П имеются такие точки, для которых не существует образов на плоскости П’. Такова, например, точка В, если проектирующая прямая SВ параллельна плоскости П’. Для устранения этого затруднения, происходящего от свойств евклидова пространства, последнее пополняют бесконечно удаленными элементами (несобственными элементами). Именно, принимают, что параллельные пряные ВS и РА’ пересекаются в бесконечно удаленной - точке В’: тогда её можно считать образом точки В на плоскости П’. Аналогично — бесконечно удалённая - С является прообразом точки С’ (рис. 2). Благодаря введению бесконечно удалённых элементов между точками плоскости П и точками плоскости П’ устанавливается взаимно однозначное соответствие, осуществляемое при помощи центральной проекции. Такое соответствие носит название перспективной коллинеации.

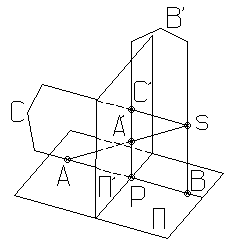
Большое практическое значение имеет вид проектирования, при котором центром проектирования является бесконечно удаленная точка S пространства (рис. 3). При этом все проектирующие прямые параллельны и проекция называется параллельной или цилиндрической. Взаимно однозначное соответствие между точками плоскостей П и П’ установленное при помощи параллельного проектирования, называемого перспективно -аффинным или родственным отображением.

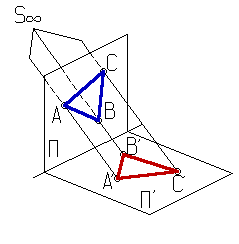
Широко применяется частный вид параллельного проектирования, когда плоскость проекции расположен перпендикулярно (ортогонально) к направлению проектирования. Проекция в этом случае называется прямоугольной или ортогональной.

Центральные и параллельные (в частности, ортогональные) проекции  находят применение в начертательной геометрии причём получаются различные виды изображений (перспективные, аксонометрические и др.). Специальные виды проектирования на плоскость, сферу и др. поверхности используются в географии, астрономии, кристаллографии, топографии и т. д. *

 

Проекция** ( от лат. projection, букв. – выбрасывание вперед) – изображение пространственных фигур на плоскости или какой-либо  другой поверхности. При этом проекция фигуры представляет собой совокупность проекций всех ее точек.**

* Математический энциклопедический словарь./ Гл. ред. Ю.В. Прохоров; Ред. кол.: С.И. Адян, Н.С. Бахвалов, В.И. Битюцков, А.П. Ершов, Л.Д. Кудрявцев, А.Л. Онищик, А.П. Юшкевич.- М.: Сов. энциклопедия, 1988. - 847 с., ил

** Политехнический словарь /Редкол.: А.Ю. Ишлинский (гл. ред.) и др. - 3 - е изд,, перераб. и доп. - М.: Советская энциклопедия, 1989. - 656 с. с ил.