Многоугольник* 

1. В математике: геометрическая фигура на плоскости, ограниченная замкнутой ломаной линией.

2. Геометрическая фигура имеющая больше четырех углов.

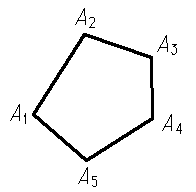
Многоугольник** замкнутая ломаная линия. Подробнее многоугольник - линия, которая получается, если взять n любых точек А₁, А₂, ..., А_n и соединить прямолинейными отрезками каждую из них с последующей, а последнюю с первой (рис.1, а, б). Точки А₁, А₂, ..., А_n называются вершинами многоугольника, а отрезки А₁А₂, А₂А₃, ..., А_n-1А_n, А_nА₁ - его сторонами. Далее рассматриваются только плоские многоугольники (т.е. предполагается, что многоугольник лежит в одной плоскости).

а	б
в	г
Рисунок 1.

 Многоугольник может сам себя пересекать (рис. 1,в), причем точки пересечения могут не быть его вершинами.

Существуют и другие точки зрения на то, что считать многоугольником. Многоугольником можно называть связную часть плоскости, вся граница которой состоит на конечного числа прямолинейных отрезков, называемых сторонами многоугольника. Многоугольник  в этом смысле может быть и многосвязной частью плоскости (рис. 1, г), т. е. такой многоугольник  может иметь «многоугольные дыры». Рассматриваются также бесконечные многоугольники — части плоскости, ограниченные конечным числом прямолинейных отрезков и конечным числом полупрямых.

Дальнейшее наложение опирается на данное выше первое определение многоугольника.

Если многоугольник  не пересекает сам себя (см., напр., рис. 1, а и б), то он разделяет совокупность всех точек плоскости, на нём не лежащих, на две части — конечную (внутреннюю) и бесконечную (внешнюю) в том смысле, что если две точки принадлежат одной из этих частей, то их можно со соединить друг с другом ломаной, не пересекающей многоугольник, а если разным частям, то нельзя. Несмотря на совершенную очевидность этого обстоятельства, строгий его вывод из аксиом геометрии довольно труден (т. н. теорема Жордана для многоугольника). Внутренняя по отношению к многоугольнику часть плоскости имеет определенную площадь. Если многоугольник  — самопересекающийся то он разрезает плоскость на определенное число кусков, из которых один бесконечный (называется внешним по отношению к многоугольнику), а остальные конечные односвязные (называется внутренними), причем  граница каждого из них есть некоторый самонепересекающийся многоугольник стороны которого суть целые стороны или части сторон, а вершины — вершины или точки самопересечения данного многоугольника. Если каждой стороне многоугольника приписать направление, т. е. указать, какую из двух определяющих её вершин мы будем считать её началом , а какую — концом, и притом так, чтобы начало каждой стороны было концом предыдущей, то получится (замкнутый) многоугольный путь, или ориентированный многоугольник. Площадь области, ограниченной самопересекающимся ориентированным многоугольник, считается положительной, если контур многоугольника обходит эту область против часовой стрелки, т. е. внутренность многоугольника остаётся слева от идущего по этому пути, и отрицательной — в противоположном случае.

Пусть многоугольник самопересекающийся и ориентированный; если из точки, лежащей во внешней во отношению к нему части плоскости, провести прямолинейный отрезок к точке, лежащей внутри одного из внутренних его кусков, многоугольник пересекает этот отрезок р раз слева направо q раз справа налево, то число р—q (целое положительное, отрицательное или нуль) не зависит от выбора внешней точки и называется коэффициентом этого куска. Сумма обычных площадей этих кусков, помноженных на их коэффициенты, считается «площадью» рассматриваемого замкнутого пути (ориентированного многоугольника).

Сумма внутренних углов любого самонепересекающегося многоугольника с n сторонами равна (n—2) 180⁰. Многоугольник. наз. выпуклым (рис. 1, а), если никакая сторона многоугольника, будучи неограниченно продолженной, не разрезает многоугольник на две части. Выпуклый многоугольник можно охарактеризовать также следующим свойством: прямолинейный отрезок, соединяющий любые две точки плоскости, лежащие внутри многоугольника, не пересекает многоугольник. 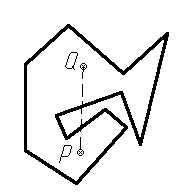Всякий выпуклый многоугольник - самонепересекающийся, но не наоборот. Например, на рис. 1, б изображён самонепересекающийся многоугольник, который не является выпуклым, так как отрезок PQ, соединяющий некоторые его внутренние точки, пересекает многоугольник.

Важнейшие многоугольники: треугольники, в частности прямоугольные, равнобедренные равносторонние (правильные); четырехугольника, в частности трапеции, параллелограммы, ромбы, прямоугольники, квадраты. Выпуклый многоугольник называется - правильным, если все его стороны равны и все внутренние углы равны. В древности умели по стороне или радиусу описанного круга строить циркулем и линейкой правильные многоугольники только в том случае, если число сторон многоугольника равно m=3_*2ⁿ, 4_*2ⁿ,  5_*2ⁿ, 3_*5_*2ⁿ, где n — любое положительное число или нуль. К. Гаусс (1804) показал, что можно построить циркулем и линейкой правильный многоугольник, когда число его сторон имеет вид m=2ⁿ _*p_1*p_2*…_*p_k, где p_1*p_2*…_*p_k - различные гауссовы простые числа, т. е. простые числа вида р=2^2s+1 (s — целое положительное число). До сих пор известны только пять таких р=3, 5, 17, 257, 65337. Из теории Галуа следует, что никаких

других правильных многоугольников кроме указанных К. Гауссом, построить циркулем и линейкой нельзя. Таким образом, построение возможно при m=3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20. 24, 32, 34, . . и невозможно при m=7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 33, …

В приведённой ниже таблице указаны радиус описанной окружности, радиус вписанной окружности и площадь правильного n-угольника (для n=3, 4, 5. 6. 8, 10),сторона которого равна k.

Число сторон	Радиус описанной окружности	Радиус вписанной окружности	Площадь
3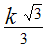
4
5
6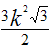
8
10

Начиная с пятиугольника, существуют также невыпуклые (самопересекающиеся, или звезчатые) в правильные многоугольники, т. е. такие, что все стороны равны и каждая следующая из сторон повёрнута в одном и том же направлении на один в тот же угол по отношению к предыдущей. Все вершины такого многоугольника также лежат на одной окружности. Такова, напр., пятиконечная звезда. На рис. 2 даны все правильные (как выпуклые так в невыпуклые) многоугольники от треугольника до семиугольника.

*Ожегов С.И. Словарь русского языка: Ок. 57000 слов под ред. чл.-корр. АН СССР Н.Ю. Шведовой. - 18-е изд., стереотип.- М.: Рус.яз., 1987 - 797 с.

** Математический энциклопедический словарь./ Гл. ред. Ю.В. Прохоров; Ред. кол.: С.И. Адян, Н.С. Бахвалов, В.И. Битюцков, А.П. Ершов, Л.Д. Кудрявцев, А.Л. Онищик, А.П. Юшкевич.- М.: Сов. энциклопедия, 1988. - 847 с., ил